Solving regex crosswords
Regex Crossword is a puzzle game to help you
practice regular expressions. I wrote a program to solve them. You can find it
on GitHub as lvh/regex-crossword. If
you're on amd64 Linux, you can try the demo binary too. This blog post
walks you through how I wrote it using logic programming.
To me this game feels more like Sudoku than a crossword. When you solve a crossword, you start by filling out the words you're certain of and use those answers as hints for the rest. Backtracking is relatively rare. In a sudoku, you might start by filling out a handful of certain boxes, but in most puzzles you quickly need to backtrack. That distinction shapes how I think of solving it: searching and backtracking is a natural fit for logic programming.
Logic programming is a niche technology, but in its sweet spot it's miraculous. I'll introduce the concept to help you recognize what sorts of problems it's good at. Worst case, you'll enjoy a cool hack. Best case you'll get the satisfaction of writing a beautiful solution to a problem some time in the future.
My programming language of choice is Clojure, and Clojure has
clojure/core.logic, a logic programming library. Because logic
programming is such a specialized tool, it's more useful to have libraries that
let you "drop in to" logic programming than to do everything in a full-blown
logic programming language.
Approach
It would not be a bad idea to read the instructions for Regex Crossword. I'll also assume you have seen some basic regular expressions. Hopefully the Clojure will be piecemeal enough you can just follow along, but reading a tutorial wouldn't hurt.
Let's take a look at the first beginner puzzle:
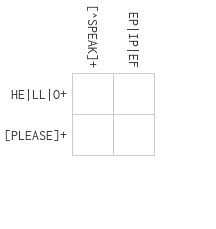
Each regex part applies to some number of unknowns (empty boxes). The first row
regex HE|LL|O+ applies to the unknowns of the first row. The first column
regex [^SPEAK]+ applies to the unknowns of the first column. Both constrain
the top left unknown: we're counting on our logic programming engine at being
convenient for expressing that "cascading" of constraints.
An unknown is just a logic variable in constraint logic programming. For brevity we'll call them "lvars" ([ell vars]).
Rows, columns (and in later puzzles hexagon lines) are all just layout. Fundamentally it's all just a regex applying to some lvars.
Breaking down regular expressions
Most regular expressions have structure, like (AB|CD)XY. We'll solve this
problem recursively: if (AB|CD)XY matches lvars p, q, r, s, then presumably
pq must match AB|CD and rs must match XY.
(There are some counterexamples to the idea that we can solve the entire problem recursively! For example, backrefs within a regex would require a second pass, and backrefs across regular expressions would require another top-level pass. We'll deal with those later. There are ties to language theory here, but that's a story for another day.)
We'll parse the regular expression into a data structure that's easier to handle. Fortunately, there's a piece of code out there that knows how to generate strings matching a given regex, which has a parser we can reuse. That parser is designed for Java's regular expression syntax. It's not quite identical to that of JavaScript, but we're hoping that the puzzles avoid those tricky edge cases for now.
To parse, we use [com.gfredericks.test.chuck.regexes :as cre].
(cre/parse "HE|LL|O+") ;; => (read: produces) {:type :alternation, :elements ({:type :concatenation, :elements ({:type :character, :character \H} {:type :character, :character \E})} {:type :concatenation, :elements ({:type :character, :character \L} {:type :character, :character \L})} {:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \O}], :bounds [1 nil]})})}
Progress! It is indeed an alternation (a or b) of a concatenation of H and E, or L and L, or the letter O one or more times.
Logic machinery
The logic programming engine is going to search a tree of possibilities for solutions that fit your constraints. Logic programming is inherently declarative: instead of telling the computer how to find the answer, we describe what the answer looks like.
An lvar that doesn't have a value assigned to it yet (it could still be anything) is called "fresh". An lvar with a definite value is called "bound". There is nothing preventing your program from returning fresh variables: that just means the answer that doesn't rely on what that lvar taking any particular value (like the x in 0x = 0).
In core.logic, a program consists of a series of expressions called goals.
(l/== a b) is a goal to make the values of a and b equal. It does not, by
itself, compare a to b or assign anything to anything. It just expresses the
idea of comparing the two. Logic programming calls this "unification".
As the engine searches the space of possible answers, sometimes a will be
equal to b already, or a will be bound and b will be fresh in which case
b will become bound to whatever a was bound to. Either way, the two
variables can be unified and the goal is said to succeed. But in many parts
of the tree this doesn't work out: a and b will already be bound to
incompatible values. In that case, the goal is said to fail. Unification is just
one of many goals, but it's the most important one in most programs including
ours.
Finally, we need a way to actually run the logic programming engine. that's
clojure.core.logic/run's job. Something like:
(l/run 1 [q] ;; run to find up to one answer with logic vars [q] (l/== q 'fred) ;; where q is unified with 'fred
... will return ('fred) (the 1-list with the symbol 'fred in it) because
there's only one answer for q that makes all the goals (here just one goal)
succeed. run takes the maximum number of answers as a parameter. Since
you're describing what the answer looks like, there might be zero, one, or any
other number of answers. Sometimes the engine will be able to prove there are no
other options (because the search was exhaustive) and it'll return fewer. Some
programs run forever, some so long it might as well be forever. run has a
sibling run* that gets you all the answers. It returns the same result,
because there's only one value for q that makes all goals succeed.
Character match
The simplest possible regular expression is just a character, which matches
itself: A. In our parse tree, this is an entry of :type :character. We'll
write a multimethod dispatching on :type to make this work so we can implement
other types later.
(defmulti re->goal :type)
A character looks like this: {:type :character, :character \L}. We'll use
destructuring to extract the :character key. In general, this multimethod will
take multiple lvars, though incidentally in the case of :character it'll
be just one, so we can destructure it as well.
(defmethod re->goal :character [{:keys [character]} [lvar]] (l/== character lvar))
We'll write a test to verify this works.
(t/deftest re->goal-character-test (t/is (= '(\A) (l/run* [q] (rcl/re->goal {:type :character :character \A} [q])))))
Alternation
Let's look at a few parse trees for some simple alternations:
(cre/parse "A|B") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :character, :character \A})} {:type :concatenation, :elements ({:type :character, :character \B})})}
Here's an example where the options are different length.
(cre/parse "AAA|B") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :character, :character \A} {:type :character, :character \A} {:type :character, :character \A})} {:type :concatenation :elements ({:type :character, :character \B})})}
It's also probably a good idea to consider something with more than two alternatives:
(cre/parse "A|B|C") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :character, :character \A})} {:type :concatenation, :elements ({:type :character, :character \B})} {:type :concatenation, :elements ({:type :character, :character \C})})}
Note the parser will always create concatenations as elements of alternations even if the element is really just a single character. We can't handle concatenations yet, so while we generally prefer things that the parser actually produces, we'll cheat with an alternation of characters first.
Alternation in logic
The obvious test to write is:
(t/deftest re->goal-alternation-test (t/is (= '(\A \B) (l/run* [q] (rcl/re->goal (cre/parse "A|B") [q])))))
... but as we saw above, that introduces concatenations. Instead:
(t/is (= '(\A \B) (l/run* [q] ;; "A|B" with the internal concatenations removed (rcl/re->goal {:type :alternation :elements [{:type :character :character \A} {:type :character :character \B}]} [q])))) (t/is (= '(\A \B \C) (l/run* [q] ;; "A|B|C" with the internal concatenations removed (rcl/re->goal {:type :alternation :elements [{:type :character :character \A} {:type :character :character \B} {:type :character :character \C}]} [q]))))
We need a way to express disjunction. Like l/and*, there's a l/or*. Once we
have that, alternation is straightforward:
(defmethod re->goal :alternation [{:keys [elements]} lvars] (l/or* (map #(re->goal % lvars) elements)))
This primer is a little unorthodox because we're walking through a problem that
requires rule generation. Most introductory texts make you build up static
rules. Disjunction is usually expressed with the macro l/conde. One difference
is that conde can express a disjunction of conjunctions in one go:
(conde [a b] [c]) ;; is equivalent to (or* [(and* a b) c])
Concatenation
We want to be able to solve squares, not just individual letters. The simplest
case is a concatenation of two characters, like AA.
(def a {:type :character :character \A}) (def aa {:type :concatenation :elements [a a]}) (t/deftest re->goal-concatenation-test (t/is (= '((\A \A)) (l/run* [p q] (rcl/re->goal aa [p q])))))
A simple implementation passes this test:
(defmethod re->goal :concatenation [{:keys [elements]} lvars] (l/and* (for [e elements v lvars] (re->goal e [v]))))
(l/and*is a function that returns a goal that succeeds when all its goals
succeed. We'd use the macro version l/all if we were explicitly writing out
our goals. Because we're generating them, it's easier to use a function.)
We're clearly abusing the fact that we happen to know that the parts are characters and therefore length 1. But the parts could be repetitions, or an alternation between concatenations each of length >1.
Distributing lvars over groups
Next, we need to find the ways lvars can be distributed over the individual elements. We know that each lvar represents a square and each square must be assigned, so we know that the sum of the lengths of the elements must be the total number of lvars.
We can actually solve this sub-problem using logic programming as well! We'll use CLP(FD), which means "constraint logic programming over finite domains".
;; [clojure.core.logic.fd :as f] (l/run* [q] (l/fresh [x y z] (l/== [x y z] q) (f/in x y z (f/interval 2 5)) (f/eq (= 10 (+ x y z))))) ;; => ([2 3 5] [3 2 5] [2 4 4] [2 5 3] [4 2 4] [3 3 4] ;; [3 4 3] [5 2 3] [4 3 3] [3 5 2] [4 4 2] [5 3 2])
As mentioned before, the approach we've taken to this problem is unique because
we're generating rules. Most logic programs have a static structure and
dynamic data, while our data informs the structure itself. We need to know how
many groups there are to know how many lvars to create with fresh. f/eq is
itself a convenience macro that rewrites "normal" Lisp-style equations (like (=
10 (+ x y z))) to a form the logic engine knows how to solve directly.
One way to solve that problem is with macros and eval, but that might impede our
ability to port to e.g. ClojureScript and native-image. Plus, I wanted to learn
more about how the finite domain magic works internally.
The main thing f/eq does here is introduce intermediate variables. The
underlying goal f/+ only takes 3 arguments: two summands and a sum result. To
express a sum over many summands you need intermediate "running total" lvars. I
wrote that:
(defn reduceo "Given a binary operator goal, return an n-ary one. If the given goal has shape `(⊕ x y z)` meaning `x ⊕ y = z`, `(reduceo ⊕ z vars)` computes `z = vars[0] ⊕ vars[1] ⊕ vars[2]...`." ;; lower case are input vars (a, b, c, d...) ;; upper case are intermediate accumulator lvars ("running totals") ;; Ω is the final result ;; a ⊕ b = A ;; A ⊕ c = B ;; ... ;; W ⊕ y = X ;; X ⊕ z = Ω ;; | | | ;; | | \_ (concat accumulators (list result)) ;; | \_ (rest lvars) ;; \_ (cons (first lvars) (butlast accumulators)) ;; ;; There are two fewer accumulators than there are input lvars. The middle ;; equations all use 2 accumulators each: one to carry the previous result and ;; one to carry it to the next equation. The first equation uses 2 input vars ;; and 1 accumulator, and the last equation uses 1 input var, 1 accumulator ;; and the result (which may be an lvar, but it's not _our_ lvar -- and in ;; common uses we expect it to be a normal value). ;; ;; We don't need the butlast because map will only use the shortest coll argument. [binop result lvars] (let [results (-> lvars count (- 2) (repeatedly l/lvar) (conj result) reverse) lefts (cons (first lvars) results) rights (rest lvars)] (l/and* (map binop lefts rights results))))
This lets us define a sum goal and a helper function that runs the logic engine for us to find all the ways we can sum up to a number, with some bounds:
(def sumo (partial reduceo f/+)) (defn summands "Find ways you can add some numbers up to a given total. For each number (summand) provide bounds `[min max]` or `nil` if you don't know. Possible assignments are returned in the same order." [total bounds] (let [lvars (repeatedly (count bounds) l/lvar) bounds-goals (map (fn [v [min max]] (f/in v (f/interval (or min 0) (or max total)))) lvars bounds)] (l/run* [q] (l/== q lvars) (l/and* bounds-goals) (sumo total lvars))))
Finally we need a way to use these weights to partition up a collection:
(defn partition-by-weights [weights coll] (loop [[weight & rest-weights] weights coll coll acc []] (if (some? weight) (recur rest-weights (drop weight coll) (conj acc (take weight coll))) acc)))
There's an alternative way to write this using appendo: (l/appendo a b c) is
like append but for lvars. You can create a version that supports multiple
lists (let's call it concato) using the same machinery:
(def concato (partial reduceo l/appendo))
In a sense concato is more direct: the lists are the lists you want, there's
no partition-by-weights to translate from your numeric answer to the list
partitions you need. With all of these goals in place we can implement
concatenation. We find each possible weight distribution, and for each
distribution, each group must match that set of lvars.
(defmethod re->goal :concatenation [{:keys [elements]} lvars] (let [n-vars (count lvars) n-elems (count elements) bounds [0 n-vars]] (l/or* (for [weights (summands n-vars (repeat n-elems bounds)) :let [lvar-groups (partition-by-weights weights lvars)]] (l/and* (map re->goal elements lvar-groups))))))
Fixing :character
What the concatenation problem tells us is that character is broken, too. Concatenation may attempt to assign 2 lvars to a single character. Right now, that returns a goal unifying the first lvar with that character: if there were more, the remaining lvars would simply go unconstrained:
(defmethod re->goal :character [{:keys [character]} [lvar]] (l/== character lvar))
We communicate a problem with a failing goal. If some goal fails, the engine
will stop exploring that branch. The always-failing goal l/fail is designed
for this sort of thing. (You can probably guess what its counterpart l/succeed
does.) The amended version looks like this:
(defmethod re->goal :character [{:keys [character]} [lvar :as lvars]] (if (-> lvars count (= 1)) (l/== character lvar) l/fail))
You could also do this in logic programming so that it's checked at runtime, but since we're generating our goals ahead of time here and only giving them to the engine at the end, we can short-circuit here.
Repetition
Sample repetition parses
Let's see what the parser does for a few simple repetitions:
(cre/parse "A{1}") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \A}], :bounds [1N 1N]})})} (cre/parse "A{1,}") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \A}], :bounds [1N nil]})})} (cre/parse "A{1,2}") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \A}], :bounds [1N 2N]})})} (cre/parse "A*") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \A}], :bounds [0 nil]})})} (cre/parse "A+") ;; => {:type :alternation, :elements ({:type :concatenation, :elements ({:type :repetition, :elements [{:type :character, :character \A}], :bounds [1 nil]})})}
This matches our expectation, since:
-
A{n}means exactly n A's -
A{m,n}means between m and n A's, inclusive -
A{n,}meansnor more A's -
A*means 0 or more A's -
A+means 1 or more A's
"No bound" is represented by nil. Some numbers are represented as just 1,
others as 1N. The latter are clojure.lang.BigInts, not longs. The parser
does this so it can support regexes with pathologically large sizes (longer than
a long, a signed 64-bit integer). We can ignore that distinction: both behave
identically for our purposes.
Implementing repetition
Repetition has a generalization of the :character behavior we fixed earlier TKTK multiple vars
(defmethod re->goal :repetition [{[elem] :elements [lower upper] :bounds} lvars] (let [n-vars (count lvars) lower (-> lower (or 0)) upper (-> upper (or n-vars) (max n-vars))] ;; Even though e.g. the empty string matches "A*", we get the lvars from the ;; structure of the puzzle, so we know all lvars have to be matched. ;; Consequence 1: 0 reps only works if there are 0 vars to match. (if (zero? n-vars) (if (zero? lower) l/succeed l/fail) (l/or* (for [reps (range (max lower 1) (inc upper)) ;; Consequence 2: can't have any leftovers: must match all parts :when (zero? (rem n-vars reps)) :let [group-size (quot n-vars reps) groups (partition group-size lvars)]] (l/and* (map (partial re->goal elem) groups)))))))
Trying to solve a few puzzles
We've done quite a bit of work but still haven't solved any real puzzles. We'd like to solve the game's own puzzles, so let's start from its internal representation. Remember the first puzzle from the beginner set:

Its internal representation looks like this:
$ jq '.[1].puzzles[0]' challenges.json { "id": "475e811a-da59-4ce8-9b80-3124b33cc041", "name": "Beatles", "patternsX": [ [ "[^SPEAK]+" ], [ "EP|IP|EF" ] ], "patternsY": [ [ "HE|LL|O+" ], [ "[PLEASE]+" ] ] }
(We'll turn the keys to kebab-case-keywords so it looks a bit more Clojure-y.)
There's something strange about the sample data: :patterns-x and :patterns-y
are both seqs of seqs of patterns. You may have expected them to be seqs of
patterns directly. This data structure choice isn't obvious until you hit a
later puzzle such as the first level in the "Double Cross" set:
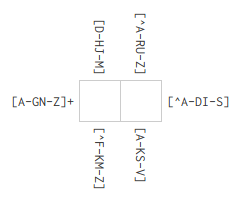
This puzzle is represented internally as:
{:id "f0f06b00-ec0a-4572-935d-7459e2a13064" :name "Telekinesis" :patterns-x [["[D-HJ-M]" "[^F-KM-Z]"] ["[^A-RU-Z]" "[A-KS-V]"]] :patterns-y [["[A-GN-Z]+" "[^A-DI-S]+"]]}
As you can see this just represents different patterns affecting the same row. Ironically while this is presumably intended to make the puzzle harder, the extra constraints probably just make the logic engine's life easier. Either way, solving means we make some lvars for each box, carve them up by rows and columns, and then apply the regex goals:
(defn solve ([puzzle] (solve puzzle nil)) ([{:keys [patterns-x patterns-y] :as puzzle} {:keys [n] :as opts :or {n 10}}] (let [n-vars (* (count patterns-x) (count patterns-y)) vars (repeatedly n-vars l/lvar) rows (partition (count patterns-x) vars) cols (apply mapv vector rows) pattern-goals (map (fn [patterns lvars] (l/and* (map #(-> % cre/parse (re->goal lvars)) patterns))) (concat patterns-x patterns-y) (concat cols rows))] (->> (l/run n [q] (l/== q vars) (l/and* pattern-goals))))))
We can use this to solve the first tutorial puzzle:
(solve {:id "272901bb-0855-4157-9b45-272935da8c93" :name "The OR symbol" :patterns-x [["A|B"]] :patterns-y [["A|Z"]]}) ;; => (((\A)))
Unfortunately, the second one has character classes, so we have to implement that next.
{:id "6915fafc-3323-484d-b801-5daac73ddb56" :name "A Range of characters" :patterns-x [["[ABC]"]] :patterns-y [["[BDF]"]]}
Character classes
Let's look at another parse:
(cre/parse "[A]") ;; => {:type :alternation, :elements [{:type :concatenation, :elements [{:type :class, :elements [{:type :class-intersection, :elements [{:type :class-union :elements [{:type :class-base :chars #{\A}}]}]}] :brackets? true}]}]}
Whoa! This parses to something a lot trickier than you might've guessed. Class
sets (intersections, unions and subtraction) are somewhat obscure set of regex
features with slightly differing support across platforms and slightly different
syntax. They're particularly useful when you have a full Unicode regex engine
and you want to say things like "match characters in this script, but not digits
or punctuation". In Java, Ruby and Python, they are spelled something like
[α&&[β]&&[γ]] where αβγ are all their own class specs.
This is a side-effect of using a parser intended for parsing Java regular expressions. JavaScript doesn't support these features. Fortunately, they're pretty easy to implement. As usual, we'll tackle the simple base case first.
(= '(\A) (l/run* [p] (rcl/re->goal {:type :class-base :chars #{\A}} [p])))
(defmethod re->goal :class-base [{:keys [chars]} [lvar :as lvars]] ;; It appears class-base will only ever have one char, but I'm writing this ;; defensively since I have no proof I've exhausted all the parser cases. (if (-> lvars count (= 1)) (l/membero lvar (vec chars)) ;; vec, bc membero doesn't work with sets l/fail))
Class union and intersection
While we could cheat implementing class union and intersection since the original JavaScript puzzle would never have them, they're trivial to express in logic, so let's just do them properly:
(t/testing "class-union" (t/is (= '(\A) (l/run* [p] (rcl/re->goal {:type :class-union :elements [{:type :class-base :chars #{\A}}]} [p])))) (t/is (= '(\A \B) (l/run* [p] (rcl/re->goal {:type :class-union :elements [{:type :class-base :chars #{\A}} {:type :class-base :chars #{\B}}]} [p]))))) (t/testing "class-intersection" (t/is (= '(\A) (l/run* [p] (rcl/re->goal {:type :class-intersection :elements [{:type :class-base :chars #{\A}}]} [p])))) (t/is (= '(\A) (l/run* [p] (rcl/re->goal {:type :class-intersection :elements [{:type :class-base :chars #{\A}} {:type :class-base :chars #{\A}}]} [p])))) (t/is (= '() (l/run* [p] (rcl/re->goal {:type :class-intersection :elements [{:type :class-base :chars #{\A}} {:type :class-base :chars #{\B}}]} [p])))))
Implemented by:
(defmethod re->goal :class-union [{:keys [elements]} lvars] (l/or* (map #(re->goal % lvars) elements))) (defmethod re->goal :class-intersection [{:keys [elements]} lvars] (l/and* (map #(re->goal % lvars) elements)))
Ranges
You're probably catching on. Implementing ranges uses a bunch of logic machinery we already use, and just a Clojure description of what a range is:
(t/is (= '(\A \B \C \D \E \F) (l/run* [q] (-> "[A-F]" cre/parse (rcl/re->goal [q])))))
Implemented by:
(defmethod re->goal :range [{:keys [elements]} [lvar :as lvars]] (if (-> lvars count (= 1)) (let [[lower upper] (map (comp int :character) elements) chars (map char (range lower (inc upper)))] (l/membero lvar chars)) l/fail))
Because ranges like A-Z0-9 are implemented using :class-union, they just
magically work.
Simple classes
"Simple classes" are things like \d, \w, \s. You know how to implement
these already.
Class negation
Class negation is actually surprisingly tricky! Many logic systems, core.logic
included, focus on positive statements. There is support for disunification
(e.g. this lvar will never be 5) with l/!=. There's also more general support
for negation as a constraint, as used here:
(defmethod re->goal :class-negation [{:keys [elements]} lvars] (l/and* (for [e elements] (l/nafc re->goal e lvars))))
Unfortunately nafc is marked as experimental and for good reason. For one, it only works if the vars are ground. Docstring claims execution will be delayed if they aren't... but that doesn't appear to be true. See LOGIC-172 for details. This problem annoyingly surfaced depending on the order clauses were evaluated in (since that changed if they were ground or not). I was able to get it to work consistently by adding a hack to make sure the vars are ground, and adding a test to make sure it would work even if this was the first clause:
(defmethod re->goal :class-negation [{:keys [elements]} lvars] (let [neg-goal (l/and* (for [e elements] (l/nafc re->goal e lvars))) domain (->> (range (int \A) (inc (int \Z))) (map char)) ground-hack (l/and* (for [v lvars] (l/membero v domain)))] (l/all ground-hack neg-goal)))
A different way to implement this would be to walk this part of the parse tree manually. Once you find a negation, you look at the rest of the parse tree and aggregate all the classes it covers. Then, you use plain negation (disunification), which has no caveats. This is what I ended up implementing; if you're interested you can read the details in the implementation.
Backrefs
Backreferences are an interesting challenge because so far we've just assumed we can recurisvely turn the regex parse tree into goals piecemeal, and backrefs break that assumption: they necessarily depend on a totally different part of the parse tree. There are two ways to address that:
- Change the implementation to produce a data structure instead of logic goals directly, and then do something eval-like later to turn the data structure into goals
- Cheat and introduce side effects to propagate within the tree walk.
The first is clearly the "good" answer. It would also enable other improvements, like tree-level performance optimization. It's also a good chunk of work, and I had spent enough time on this weekend project already. So, instead, I did the hacky side-effecty version. This turned out to be tricky to implement not from a logic perspective (that part is easy) but because the underlying parser I had forklifted was from a project that didn't support backrefs, and so it didn't bother to parse them out correctly. You can see how I hacked around that in the implementation.
Conclusion
This introduction was a little unorthodox. Most texts focus on introducing
different primitives, have you write small static rules and build up from there.
You'll see conde long before anyone talks to you about or*.
Negation-as-failure, which we used for classes, is exotic and non-relational.
The way we implemented backrefs works but is inelegant. That's all just a
consequence of the problem we solved, not a principled stance on how to use
core.logic let alone teach it. Reading The Little Schemer is still a
good idea if you want to learn to write your own programs.
(If you want a logic program where the goals are not fixed in advance, you might want to just stick to the JVM so there are no restrictions on eval use. I haven't tried running core.logic on sci.)
Next steps
These are things I thought were neat but didn't make sense in the original text.
Running programs backwards
A truly mind-bending feature of relational programs is that they can be ran "backwards". Usually, you write a program "forwards": it has some inputs and you expect some outputs. If you write your logic program a particular way, it doesn't actually know what's an input and what's an output, and so you can give it an "output" and it will come up with "inputs" that would have led to that output. This post did not demonstrate that, but it's one of the better hooks I've found to get people excited about logic programming. I could not give this talk better than Will Byrd presenting miniKanren. I won't spoil the ending, but go watch that talk.
Our program does not work that way. All our "inputs" are rules, all our lvars are the same kind (unknown boxes), so running it "backwards" doesn't really mean anything. It could, if our parser and rule generation were also fully relational. In that case, we could fill out some boxes and our program would tell us progressively more creative regular expressions that would match them. Instead of a puzzle solver, we would have written a puzzle creator.
Palindromes
Some puzzles have hints that help you solve them. Usually they're thematic cues, (e.g. "Hamlet") which are hard to tell a logic engine about. Structural cues are easy. For example, if you think some lines should be palindromes, you can just add the following constraint:
(l/all* (map (fn [vars] (l/== vars (reverse vars))) lines))
If evaluated at the right time, this should constrain the search tree. It's tricky to make sure that happens without measurement and fiddling.
Thematic cues
If you really wanted to add thematic cues, e.g. "Hamlet", you could grab the Wikipedia page, use something like TF/IDF to find important words, filter by the appropriate size, and introduce them as constraints. I don't expect this will speed anything up much even if you discount the initial step.
Hexagon shaped puzzles
I made these work, but didn't hook it up to the solver permanently (mostly because I lost interest). I like hex grids a lot, but they're not interesting from a logic perspective so I didn't cover them in this post. You can check out the implementation but be warned: it's mostly just some tedious bean counting.